This page was generated from examples/ConsBequestModel/example_WarmGlowBequestPort.ipynb.
Interactive online version: . Download notebook.

Warm-Glow Bequest Motive and Portfolio Choice

This notebook only provides examples and does not explain the model. It will be revised and expanded in the near future.

from copy import copy
from time import time

import matplotlib.pyplot as plt
import pandas as pd

from HARK.Calibration.Income.IncomeTools import (
    CGM_income,
    parse_income_spec,
    parse_time_params,
)
from HARK.Calibration.life_tables.us_ssa.SSATools import parse_ssa_life_table
from HARK.Calibration.SCF.WealthIncomeDist.SCFDistTools import (
    income_wealth_dists_from_scf,
)
from HARK.ConsumptionSaving.ConsBequestModel import (
    BequestWarmGlowPortfolioType,
    init_portfolio_bequest,
)
from HARK.utilities import plot_funcs

# First define the portfolio params similar to the notebook solution for that agent type
ConsPortfolioDict = {
    # Parameters shared with the Perfect foresight consumer type
    "CRRA": 5.0,  # Coefficient of relative risk aversion,
    "Rfree": [1.03],  # Interest factor on assets
    "DiscFac": 0.90,  # Intertemporal discount factor
    "LivPrb": [0.98],  # Survival probability
    "PermGroFac": [1.01],  # Permanent income growth factor
    "BoroCnstArt": 0.0,  # Artificial borrowing constraint
    # Maximum number of grid points to allow in cFunc (should be large)
    "MaxKinks": 400,
    # Number of agents of this type (only matters for simulation)
    "AgentCount": 10000,
    # Mean of log initial assets (only matters for simulation)
    "kLogInitMean": 0.0,
    # Standard deviation of log initial assets (only for simulation)
    "kNrmInitStd": 1.0,
    # Mean of log initial permanent income (only matters for simulation)
    "pLogInitMean": 0.0,
    # Standard deviation of log initial permanent income (only matters for simulation)
    "pLogInitStd": 0.0,
    # Aggregate permanent income growth factor: portion of PermGroFac attributable to aggregate productivity growth (only matters for simulation)
    "PermGroFacAgg": 1.0,
    "T_age": None,  # Age after which simulated agents are automatically killed
    "T_cycle": 1,  # Number of periods in the cycle for this agent type
    "PerfMITShk": False,  # Do Perfect Foresight MIT Shock: Forces Newborns to follow solution path of the agent he/she replaced when True
    # assets above grid parameters
    "aXtraMin": 0.001,  # Minimum end-of-period "assets above minimum" value
    "aXtraMax": 100,  # Maximum end-of-period "assets above minimum" value
    # Exponential nesting factor when constructing "assets above minimum" grid
    "aXtraNestFac": 1,
    "aXtraCount": 200,  # Number of points in the grid of "assets above minimum"
    "aXtraExtra": [
        None,
    ],  # Some other value of "assets above minimum" to add to the grid, not used
    # Income process variables
    "PermShkStd": [0.1],  # Standard deviation of log permanent income shocks
    "PermShkCount": 7,  # Number of points in discrete approximation to permanent income shocks
    "TranShkStd": [0.1],  # Standard deviation of log transitory income shocks
    "TranShkCount": 7,  # Number of points in discrete approximation to transitory income shocks
    "UnempPrb": 0.05,  # Probability of unemployment while working
    "UnempPrbRet": 0.005,  # Probability of "unemployment" while retired
    "IncUnemp": 0.3,  # Unemployment benefits replacement rate
    "IncUnempRet": 0.0,  # "Unemployment" benefits when retired
    "tax_rate": 0.0,  # Flat income tax rate
    "vFuncBool": False,  # Whether to calculate the value function during solution
    # Use cubic spline interpolation when True, linear interpolation when False
    "CubicBool": False,
    # Use permanent income neutral measure (see Harmenberg 2021) during simulations when True.
    "neutral_measure": False,
    # Whether Newborns have transitory shock. The default is False.
    "NewbornTransShk": False,
    # Flag for whether to optimize risky share on a discrete grid only
}

birth_age = 25
death_age = 90
adjust_infl_to = 1992
income_calib = CGM_income
education = "College"

# Income specification
income_params = parse_income_spec(
    age_min=birth_age,
    age_max=death_age,
    adjust_infl_to=adjust_infl_to,
    **income_calib[education],
    SabelhausSong=True,
)

# Initial distribution of wealth and permanent income
dist_params = income_wealth_dists_from_scf(
    base_year=adjust_infl_to,
    age=birth_age,
    education=education,
    wave=1995,
)

# We need survival probabilities only up to death_age-1, because survival
# probability at death_age is 1.
liv_prb = parse_ssa_life_table(
    female=True,
    cross_sec=True,
    year=2004,
    age_min=birth_age,
    age_max=death_age,
)

portfolio_params = {  # Attributes specific to the Portfolio consumer
    "RiskyAvg": 1.08,  # Average return of the risky asset
    "RiskyStd": 0.20,  # Standard deviation of (log) risky returns
    "RiskyCount": 5,  # Number of integration nodes to use in approximation of risky returns
    "ShareCount": 25,  # Number of discrete points in the risky share approximation
    # Probability that the agent can adjust their risky portfolio share each period
    "AdjustPrb": 1.0,
    "DiscreteShareBool": False,
}

# Parameters related to the number of periods implied by the calibration
time_params = parse_time_params(age_birth=birth_age, age_death=death_age)

# Update all the new parameters
params = copy(init_portfolio_bequest)
params.update(time_params)
params.update(dist_params)
params.update(income_params)
params.update(portfolio_params)
params.update({"LivPrb": [1.0] * len(liv_prb)})
params["Rfree"] = len(liv_prb) * [params["Rfree"][0]]

# Make and solve an idiosyncratic shocks consumer with a finite lifecycle
Agent = BequestWarmGlowPortfolioType(**params)
# Make this consumer live a sequence of periods exactly once
Agent.cycles = 1
print(Agent.BeqFac)

40.0

start_time = time()
Agent.solve()
end_time = time()
print(f"Solving a lifecycle consumer took {end_time - start_time} seconds.")
Agent.unpack("cFuncAdj")

Solving a lifecycle consumer took 2.655607223510742 seconds.

# Plot the consumption functions
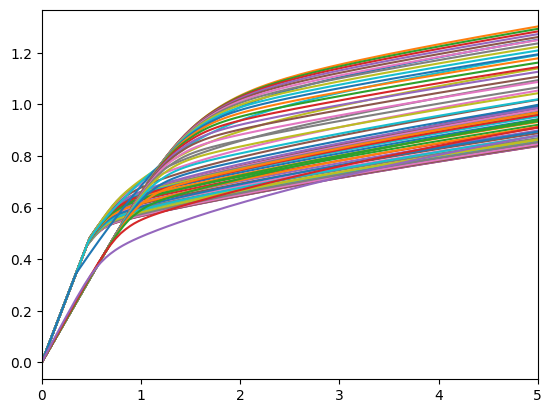
print("Consumption functions")
plot_funcs(Agent.cFuncAdj, 0, 5)

Consumption functions

# Number of LifecycleExamples and periods in the simulation.
Agent.AgentCount = 500
Agent.T_sim = 200

# Set up the variables we want to keep track of.
Agent.track_vars = ["aNrm", "cNrm", "pLvl", "t_age", "mNrm"]

# Run the simulations
Agent.initialize_sim()
Agent.simulate()

raw_data = {
    "Age": Agent.history["t_age"].flatten() + birth_age - 1,
    "pIncome": Agent.history["pLvl"].flatten(),
    "nrmM": Agent.history["mNrm"].flatten(),
    "nrmC": Agent.history["cNrm"].flatten(),
}

Data = pd.DataFrame(raw_data)
Data["Cons"] = Data.nrmC * Data.pIncome
Data["M"] = Data.nrmM * Data.pIncome

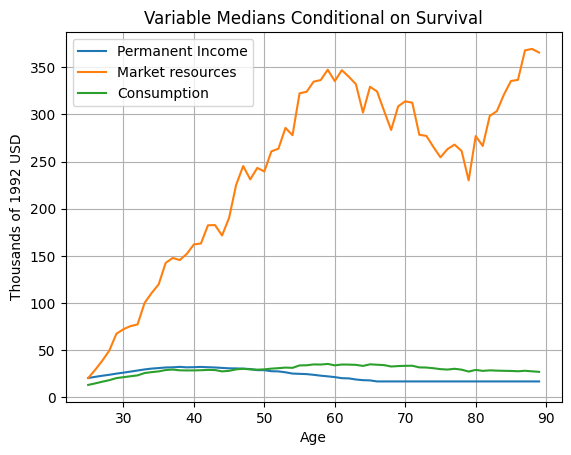
# Find the mean of each variable at every age
AgeMeans = Data.groupby(["Age"]).median().reset_index()

plt.figure()
plt.plot(AgeMeans.Age, AgeMeans.pIncome, label="Permanent Income")
plt.plot(AgeMeans.Age, AgeMeans.M, label="Market resources")
plt.plot(AgeMeans.Age, AgeMeans.Cons, label="Consumption")
plt.legend()
plt.xlabel("Age")
plt.ylabel(f"Thousands of {adjust_infl_to} USD")
plt.title("Variable Medians Conditional on Survival")
plt.grid()