This page was generated from examples/ConsMarkovModel/MarkovConsumerType.ipynb.
Interactive online version: . Download notebook.

Discrete State with Markov Transitions

from copy import copy, deepcopy
from time import process_time

import numpy as np
import matplotlib.pyplot as plt

from HARK.ConsumptionSaving.ConsMarkovModel import (
    MarkovConsumerType,
    init_indshk_markov,
)
from HARK.distributions import DiscreteDistributionLabeled
from HARK.utilities import plot_funcs

mystr = lambda number: f"{number:.4f}"
do_simulation = True

This module defines consumption-saving models in which an agent has CRRA utility over consumption, geometrically discounts future utility flows and expects to experience transitory and permanent shocks to his/her income. Moreover, in any given period s/he is in exactly one of several discrete states. This state evolves from period to period according to a Markov process.

In this model, an agent is very similar to the one in the “idiosyncratic shocks” model of ConsIndShockModel, except that here, an agent’s income distribution (\(F_{\psi t},F_{\theta t}\)), permanent income growth rate \(\Gamma_{t+1}\) and interest factor \(R\) are all functions of the Markov state and might vary across states.

The agent’s problem can be written in Bellman form as:

\begin{eqnarray*} v_t(m_t,s_t) &=& \max_{c_t} u(c_t) + \beta (1-\mathsf{D}_{t+1}) \mathbb{E} [v_{t+1}(m_{t+1}, s_{t+1}) ], \\ a_t &=& m_t - c_t, \\ a_t &\geq& \underline{a}, \\ m_{t+1} &=& \frac{R(s_{t+1})}{\Gamma(s_{t+1})\psi_{t+1}} a_t + \theta_{t+1}, \\ \theta_{t} \sim F_{\theta t}(s_t), &\qquad& \psi_{t} \sim F_{\psi t}(s_t), \mathbb{E} [F_{\psi t}(s_t)] = 1, \\ Prob[s_{t+1}=j| s_t=i] &=& \triangle_{ij}, \\ u(c) &=& \frac{c^{1-\rho}}{1-\rho} \end{eqnarray*}

The Markov matrix \(\triangle\) is giving transition probabilities from current state \(i\) to future state \(j\).

The one period problem for this model is solved by the function solveConsMarkov. The class MarkovConsumerType extends IndShockConsumerType to represents agents in this model.

To solve an instance of this class, the same attributes as for IndShockConsumerType are required, except for one as described below:

Additional model input to solve an instance of MarkovConsumerType

Param	Description	Code	Value	Constructed
\(\triangle\)	Discrete state transition probability matrix	MrkvArray		\(\surd\)

The attribute MrkvArray is a numpy.array of size (\(N_s\), \(N_s\)) corresponding to the number of discrete states.

Note that MrkvArray is am element of time_inv, so that the same transition probabilities are used for each period. However, it can be moved to time_vary and specified as a list of arrays instead.

The attributes Rfree, PermGroFac and IncomeDstn should be specified as arrays or lists with \(N_s\) elements for each period.

Solve MarkovConsumerType

When the solve() method of a MarkovConsumerType is invoked, the solution attribute is populated with a list of ConsumerSolution objects, which each have the same attributes as the “idiosyncratic shocks” model. However, each attribute is now a list (or array) whose elements are state-conditional values of that object.

For example, in a model with 4 discrete states, each the cFunc attribute of each element of solution is a length-4 list whose elements are state-conditional consumption functions. That is, cFunc[2] is the consumption function when \(s_t = 2\).

ConsMarkovModel is compatible with cubic spline interpolation for the consumption functions, soCubicBool = True will not generate an exception. The problem is solved using the method of endogenous gridpoints, which is moderately more complicated than in the basic ConsIndShockModel.

Several variant examples of the model will be illustrated below:

1. Model with serially correlated unemployment

2. Model with period of “unemployment immunity”

3. Model with serially correlated permanent income growth

4. Model with serially correlated interest factor

1. Serial Unemployment

Let’s create a consumer similar to the one in “idiosyncratic shock” model but who faces serially correlated unemployment during boom or bust cycles of the economy.

# Define the Markov transition matrix for serially correlated unemployment
unemp_length = 5  # Averange length of unemployment spell
urate_good = 0.05  # Unemployment rate when economy is in good state
urate_bad = 0.12  # Unemployment rate when economy is in bad state
bust_prob = 0.01  # Probability of economy switching from good to bad
recession_length = 20  # Averange length of bad state
p_reemploy = 1.0 / unemp_length
p_unemploy_good = p_reemploy * urate_good / (1 - urate_good)
p_unemploy_bad = p_reemploy * urate_bad / (1 - urate_bad)
boom_prob = 1.0 / recession_length
MrkvArray = np.array(
    [
        [
            (1 - p_unemploy_good) * (1 - bust_prob),
            p_unemploy_good * (1 - bust_prob),
            (1 - p_unemploy_good) * bust_prob,
            p_unemploy_good * bust_prob,
        ],
        [
            p_reemploy * (1 - bust_prob),
            (1 - p_reemploy) * (1 - bust_prob),
            p_reemploy * bust_prob,
            (1 - p_reemploy) * bust_prob,
        ],
        [
            (1 - p_unemploy_bad) * boom_prob,
            p_unemploy_bad * boom_prob,
            (1 - p_unemploy_bad) * (1 - boom_prob),
            p_unemploy_bad * (1 - boom_prob),
        ],
        [
            p_reemploy * boom_prob,
            (1 - p_reemploy) * boom_prob,
            p_reemploy * (1 - boom_prob),
            (1 - p_reemploy) * (1 - boom_prob),
        ],
    ],
)

# Make a consumer with serially correlated unemployment, subject to boom and bust cycles
init_serial_unemployment = copy(init_indshk_markov)
init_serial_unemployment["MrkvArray"] = [MrkvArray]
init_serial_unemployment["UnempPrb"] = np.zeros(2)
# Income process is overwritten below to make income distribution when employed
init_serial_unemployment["global_markov"] = False
init_serial_unemployment["Rfree"] = np.array([1.03, 1.03, 1.03, 1.03])
init_serial_unemployment["LivPrb"] = [np.array([0.98, 0.98, 0.98, 0.98])]
init_serial_unemployment["PermGroFac"] = [np.array([1.01, 1.01, 1.01, 1.01])]
SerialUnemploymentExample = MarkovConsumerType(**init_serial_unemployment)
SerialUnemploymentExample.cycles = 0
SerialUnemploymentExample.vFuncBool = False  # for easy toggling here

# Replace the default (lognormal) income distribution with a custom one
employed_income_dist = DiscreteDistributionLabeled(
    pmv=np.ones(1),
    atoms=np.array([[1.0], [1.0]]),
    var_names=["PermShk", "TranShk"],
)  # Definitely get income
unemployed_income_dist = DiscreteDistributionLabeled(
    pmv=np.ones(1),
    atoms=np.array([[1.0], [0.0]]),
    var_names=["PermShk", "TranShk"],
)  # Definitely don't
SerialUnemploymentExample.IncShkDstn = [
    [
        employed_income_dist,
        unemployed_income_dist,
        employed_income_dist,
        unemployed_income_dist,
    ],
]
SerialUnemploymentExample.assign_parameters(MrkvArray=[MrkvArray])

# Interest factor, permanent growth rates, and survival probabilities are constant arrays
SerialUnemploymentExample.assign_parameters(Rfree=[np.array(1.03 * np.ones(4))])
SerialUnemploymentExample.PermGroFac = [1.0 * np.ones(4)]
SerialUnemploymentExample.LivPrb = [0.98 * np.ones(4)]

# Solve the serial unemployment consumer's problem and display solution
start_time = process_time()
SerialUnemploymentExample.solve()
end_time = process_time()
print(
    "Solving a Markov consumer with serially correlated unemployment took "
    + mystr(end_time - start_time)
    + " seconds.",
)
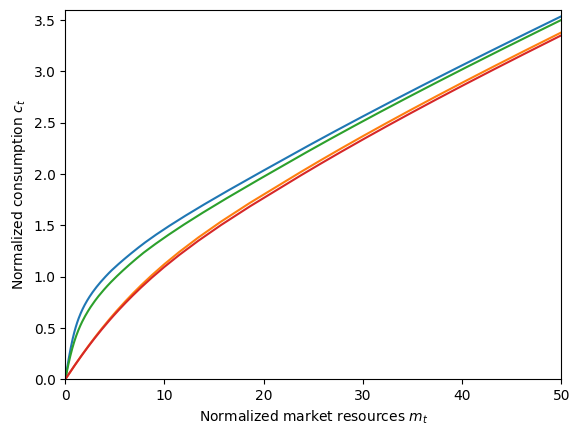
print("Consumption functions for each discrete state:")
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 3.6)
plot_funcs(SerialUnemploymentExample.solution[0].cFunc, 0.0, 50)
if SerialUnemploymentExample.vFuncBool:
    print("Value functions for each discrete state:")
    plot_funcs(SerialUnemploymentExample.solution[0].vFunc, 0.5, 50)

Solving a Markov consumer with serially correlated unemployment took 0.3594 seconds.
Consumption functions for each discrete state:

# Simulate some data; results stored in cHist, mNrm_hist, cNrm_hist, and Mrkv_hist
if do_simulation:
    SerialUnemploymentExample.T_sim = 120
    SerialUnemploymentExample.MrkvPrbsInit = [0.25, 0.25, 0.25, 0.25]
    SerialUnemploymentExample.track_vars = ["mNrm", "cNrm"]
    SerialUnemploymentExample.make_shock_history()  # This is optional
    SerialUnemploymentExample.initialize_sim()
    SerialUnemploymentExample.simulate()

2. Unemployment immunity for a fixed period

Let’s create a consumer similar to the one in “idiosyncratic shock” model but who occasionally gets “unemployment immunity” for a fixed period in an economy subject to boom and bust cycles.

# Make a consumer who occasionally gets "unemployment immunity" for a fixed period
UnempPrb = 0.05  # Probability of becoming unemployed each period
ImmunityPrb = 0.01  # Probability of becoming "immune" to unemployment
ImmunityT = 6  # Number of periods of immunity

StateCount = ImmunityT + 1  # Total number of Markov states
IncomeDstnReg = DiscreteDistributionLabeled(
    pmv=np.array([1 - UnempPrb, UnempPrb]),
    atoms=np.array([[1.0, 1.0], [1.0 / (1.0 - UnempPrb), 0.0]]),
    var_names=["PermShk", "TranShk"],
)  # Ordinary income distribution
IncomeDstnImm = DiscreteDistributionLabeled(
    pmv=np.array([1.0]),
    atoms=np.array([[1.0], [1.0]]),
    var_names=["PermShk", "TranShk"],
)
IncomeDstn = [IncomeDstnReg] + ImmunityT * [
    IncomeDstnImm,
]  # Income distribution for each Markov state, in a list

# Make the Markov transition array.  MrkvArray[i,j] is the probability of transitioning
# to state j in period t+1 from state i in period t.
MrkvArray = np.zeros((StateCount, StateCount))
MrkvArray[0, 0] = (
    1.0 - ImmunityPrb
)  # Probability of not becoming immune in ordinary state: stay in ordinary state
MrkvArray[0, ImmunityT] = (
    ImmunityPrb  # Probability of becoming immune in ordinary state: begin immunity periods
)
for j in range(ImmunityT):
    MrkvArray[j + 1, j] = (
        1.0  # When immune, have 100% chance of transition to state with one fewer immunity periods remaining
    )

init_unemployment_immunity = copy(init_indshk_markov)
init_unemployment_immunity["MrkvArray"] = [MrkvArray]
ImmunityExample = MarkovConsumerType(**init_unemployment_immunity)
ImmunityExample.assign_parameters(MrkvArray=[MrkvArray])
ImmunityExample.assign_parameters(
    Rfree=[
        np.array(np.array(StateCount * [1.03]))
    ],  # Interest factor same in all states
    PermGroFac=[
        np.array(StateCount * [1.01]),
    ],  # Permanent growth factor same in all states
    LivPrb=[np.array(StateCount * [0.98])],  # Same survival probability in all states
    BoroCnstArt=None,  # No artificial borrowing constraint
    cycles=0,
)  # Infinite horizon
ImmunityExample.IncShkDstn = [IncomeDstn]

# Solve the unemployment immunity problem and display the consumption functions
start_time = process_time()
ImmunityExample.solve()
end_time = process_time()
print(
    'Solving an "unemployment immunity" consumer took '
    + mystr(end_time - start_time)
    + " seconds.",
)
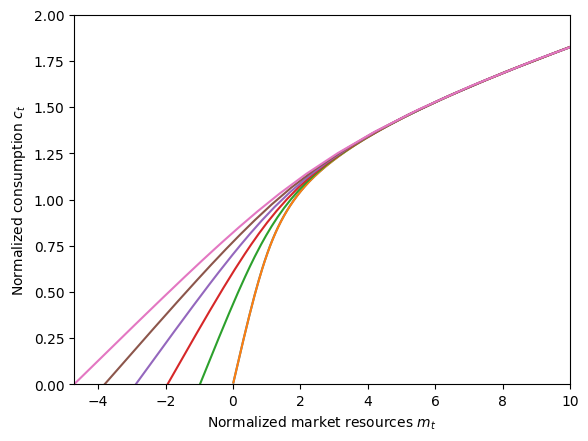
print("Consumption functions for each discrete state:")
mNrmMin = np.min([ImmunityExample.solution[0].mNrmMin[j] for j in range(StateCount)])
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 2.0)
plot_funcs(ImmunityExample.solution[0].cFunc, mNrmMin, 10)

Solving an "unemployment immunity" consumer took 0.3281 seconds.
Consumption functions for each discrete state:

C:\Users\Matthew\Documents\GitHub\HARK\HARK\interpolation.py:2145: RuntimeWarning: All-NaN slice encountered
  y = self.compare(fx, axis=1)

3. Serial permanent income growth

Let’s create a consumer similar to the one in “idiosyncratic shock” model but who faces serially correlated permanent income growth in an economy subject to boom and bust cycles.

# Make a consumer with serially correlated permanent income growth
UnempPrb = 0.05  # Unemployment probability
StateCount = 5  # Number of permanent income growth rates
Persistence = (
    0.5  # Probability of getting the same permanent income growth rate next period
)

IncomeDstnReg = DiscreteDistributionLabeled(
    pmv=np.array([1 - UnempPrb, UnempPrb]),
    atoms=np.array([[1.0, 1.0], [1.0, 0.0]]),
    var_names=["PermShk", "TranShk"],
)
IncomeDstn = StateCount * [
    IncomeDstnReg,
]  # Same simple income distribution in each state

# Make the state transition array for this type: Persistence probability of remaining in the same state, equiprobable otherwise
MrkvArray = Persistence * np.eye(StateCount) + (1.0 / StateCount) * (
    1.0 - Persistence
) * np.ones((StateCount, StateCount))

init_serial_growth = copy(init_indshk_markov)
init_serial_growth["MrkvArray"] = [MrkvArray]
SerialGroExample = MarkovConsumerType(**init_serial_growth)
SerialGroExample.assign_parameters(MrkvArray=[MrkvArray])
SerialGroExample.assign_parameters(
    Rfree=[
        np.array(
            np.array(StateCount * [1.03]),
        )
    ],  # Same interest factor in each Markov state
    PermGroFac=[
        np.array([0.97, 0.99, 1.01, 1.03, 1.05]),
    ],  # Different permanent growth factor in each Markov state
    LivPrb=[np.array(StateCount * [0.98])],  # Same survival probability in all states
    cycles=0,
)
SerialGroExample.IncShkDstn = [IncomeDstn]

# Solve the serially correlated permanent growth shock problem and display the consumption functions
start_time = process_time()
SerialGroExample.solve()
end_time = process_time()
print(
    "Solving a serially correlated growth consumer took "
    + mystr(end_time - start_time)
    + " seconds.",
)
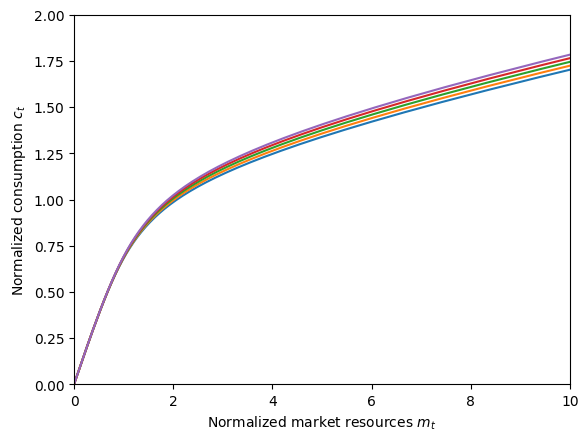
print("Consumption functions for each discrete state:")
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 2.0)
plot_funcs(SerialGroExample.solution[0].cFunc, 0, 10)

Solving a serially correlated growth consumer took 0.2500 seconds.
Consumption functions for each discrete state:

4. Serial Interest factor

Finally, suppose that the consumer faces a interest factor serially correlated while his/her permanent income growth rate is constant.

# Make a consumer with serially correlated interest factors
SerialRExample = deepcopy(SerialGroExample)  # Same as the last problem...
SerialRExample.assign_parameters(
    PermGroFac=[
        np.array(StateCount * [1.01]),
    ],  # ...but now the permanent growth factor is constant...
    Rfree=[np.array([1.01, 1.02, 1.03, 1.04, 1.05])],
)  # ...and the interest factor is what varies across states

# Solve the serially correlated interest rate problem and display the consumption functions
start_time = process_time()
SerialRExample.solve()
end_time = process_time()
print(
    "Solving a serially correlated interest consumer took "
    + mystr(end_time - start_time)
    + " seconds.",
)
print("Consumption functions for each discrete state:")
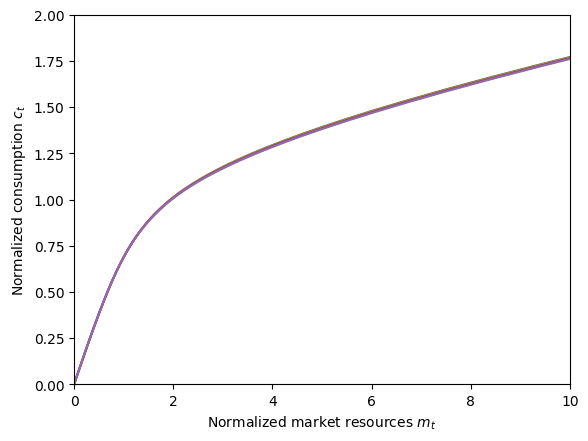
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 2.0)
plot_funcs(SerialRExample.solution[0].cFunc, 0, 10)

Solving a serially correlated interest consumer took 0.2500 seconds.
Consumption functions for each discrete state: