This page was generated from examples/ConsRiskyContribModel/RiskyContribConsumerType.ipynb.
Interactive online version: . Download notebook.

“Risky Contribution” Model

This notebook doesn’t actually explain the model yet; sorry!

from time import time

import numpy as np

from HARK.ConsumptionSaving.ConsRiskyContribModel import (
    RiskyContribConsumerType,
    init_risky_contrib,
)

def plot_slices_3d(
    functions,
    bot_x,
    top_x,
    y_slices,
    N=300,
    y_name=None,
    titles=None,
    ax_labs=None,
):
    import matplotlib.pyplot as plt

    if type(functions) == list:
        function_list = functions
    else:
        function_list = [functions]

    nfunc = len(function_list)

    # Initialize figure and axes
    fig = plt.figure(figsize=plt.figaspect(1.0 / nfunc))

    # Create x grid
    x = np.linspace(bot_x, top_x, N, endpoint=True)

    for k in range(nfunc):
        ax = fig.add_subplot(1, nfunc, k + 1)

        for y in y_slices:
            if y_name is None:
                lab = ""
            else:
                lab = y_name + "=" + str(y)

            z = function_list[k](x, np.ones_like(x) * y)
            ax.plot(x, z, label=lab)

        if ax_labs is not None:
            ax.set_xlabel(ax_labs[0])
            ax.set_ylabel(ax_labs[1])

        # ax.imshow(Z, extent=[bottom[0],top[0],bottom[1],top[1]], origin='lower')
        # ax.colorbar();
        if titles is not None:
            ax.set_title(titles[k])

        ax.set_xlim([bot_x, top_x])

        if y_name is not None:
            ax.legend()

    plt.show()


def plot_slices_4d(
    functions,
    bot_x,
    top_x,
    y_slices,
    w_slices,
    N=300,
    slice_names=None,
    titles=None,
    ax_labs=None,
):
    import matplotlib.pyplot as plt

    if type(functions) == list:
        function_list = functions
    else:
        function_list = [functions]

    nfunc = len(function_list)
    nws = len(w_slices)

    # Initialize figure and axes
    fig = plt.figure(figsize=plt.figaspect(1.0 / nfunc))

    # Create x grid
    x = np.linspace(bot_x, top_x, N, endpoint=True)

    for j in range(nws):
        w = w_slices[j]

        for k in range(nfunc):
            ax = fig.add_subplot(nws, nfunc, j * nfunc + k + 1)

            for y in y_slices:
                if slice_names is None:
                    lab = ""
                else:
                    lab = (
                        slice_names[0]
                        + "="
                        + str(y)
                        + ","
                        + slice_names[1]
                        + "="
                        + str(w)
                    )

                z = function_list[k](x, np.ones_like(x) * y, np.ones_like(x) * w)
                ax.plot(x, z, label=lab)

            if ax_labs is not None:
                ax.set_xlabel(ax_labs[0])
                ax.set_ylabel(ax_labs[1])

            # ax.imshow(Z, extent=[bottom[0],top[0],bottom[1],top[1]], origin='lower')
            # ax.colorbar();
            if titles is not None:
                ax.set_title(titles[k])

            ax.set_xlim([bot_x, top_x])

            if slice_names is not None:
                ax.legend()

    plt.show()

# Solve an infinite horizon version

# Get initial parameters
par_infinite = init_risky_contrib.copy()
# And make the problem infinite horizon
par_infinite["cycles"] = 0
# and sticky
par_infinite["AdjustPrb"] = [1.0]
# and with a withdrawal tax
par_infinite["WithdrawTax"] = [0.1]

par_infinite["DiscreteShareBool"] = False
par_infinite["vFuncBool"] = False

# Create agent and solve it.
inf_agent = RiskyContribConsumerType(tolerance=1e-3, **par_infinite)
print("Now solving infinite horizon version; this will take a minute.")
t0 = time()
inf_agent.solve(verbose=False)
t1 = time()
print("Converged!")
print("Solving took " + str(t1 - t0) + " seconds.")

# Plot policy functions
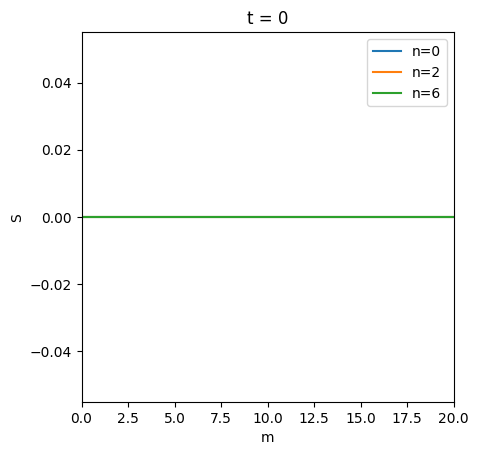
periods = [0]
n_slices = [0, 2, 6]
mMax = 20

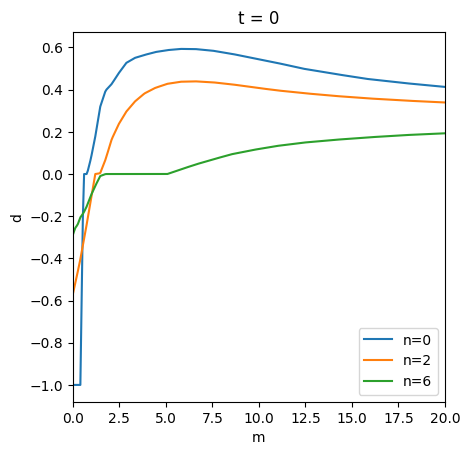
dfracFunc = [inf_agent.solution[t].stage_sols["Reb"].dfracFunc_Adj for t in periods]
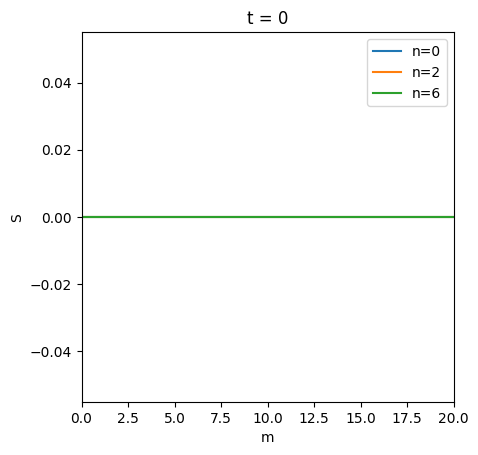
ShareFunc = [inf_agent.solution[t].stage_sols["Sha"].ShareFunc_Adj for t in periods]
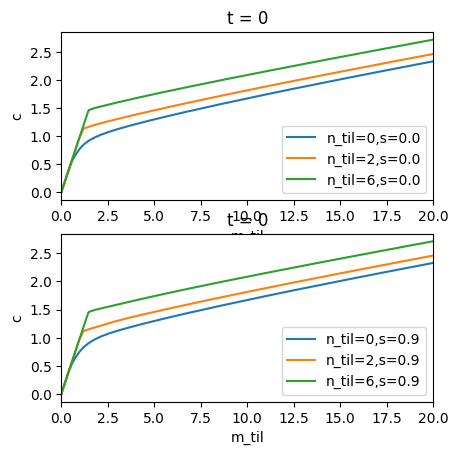
cFuncFxd = [inf_agent.solution[t].stage_sols["Cns"].cFunc for t in periods]

# Rebalancing
plot_slices_3d(
    dfracFunc,
    0,
    mMax,
    y_slices=n_slices,
    y_name="n",
    titles=["t = " + str(t) for t in periods],
    ax_labs=["m", "d"],
)
# Share
plot_slices_3d(
    ShareFunc,
    0,
    mMax,
    y_slices=n_slices,
    y_name="n",
    titles=["t = " + str(t) for t in periods],
    ax_labs=["m", "S"],
)

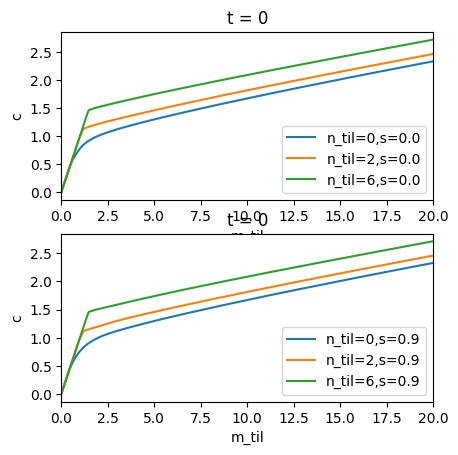
# Consumption
shares = [0.0, 0.9]
plot_slices_4d(
    cFuncFxd,
    0,
    mMax,
    y_slices=n_slices,
    w_slices=shares,
    slice_names=["n_til", "s"],
    titles=["t = " + str(t) for t in periods],
    ax_labs=["m_til", "c"],
)

Now solving infinite horizon version; this will take a minute.
Converged!
Solving took 54.27440142631531 seconds.

Finished cycle #37 in 0.23799729347229004 seconds, solution distance = 0.22001247043174033
Finished cycle #38 in 0.24099016189575195 seconds, solution distance = 0.2041307958435148
Finished cycle #39 in 0.24204635620117188 seconds, solution distance = 0.1895511158691363
Finished cycle #40 in 0.24039459228515625 seconds, solution distance = 0.17614114810584525
Finished cycle #41 in 0.24804925918579102 seconds, solution distance = 0.16379223371877671
Finished cycle #42 in 0.23607158660888672 seconds, solution distance = 0.15240148828154432
Finished cycle #43 in 0.24167418479919434 seconds, solution distance = 0.14188487999826904
Finished cycle #44 in 0.24086308479309082 seconds, solution distance = 0.13216482757643888
Finished cycle #45 in 0.2350912094116211 seconds, solution distance = 0.12317119440462676
Finished cycle #46 in 0.23387527465820312 seconds, solution distance = 0.1148412372958667
Finished cycle #47 in 0.245802640914917 seconds, solution distance = 0.1071190115202647
Finished cycle #48 in 0.24527525901794434 seconds, solution distance = 0.09995443417609451
Finished cycle #49 in 0.23836779594421387 seconds, solution distance = 0.09330220644322651
Finished cycle #50 in 0.2500934600830078 seconds, solution distance = 0.08712305238126916
Finished cycle #51 in 0.2407543659210205 seconds, solution distance = 0.08137793451099284
Finished cycle #52 in 0.24480748176574707 seconds, solution distance = 0.07603087196451241
Finished cycle #53 in 0.24602246284484863 seconds, solution distance = 0.07105207269190572
Finished cycle #54 in 0.24190545082092285 seconds, solution distance = 0.06641377226958056
Finished cycle #55 in 0.2417135238647461 seconds, solution distance = 0.06209046840455912
Finished cycle #56 in 0.23904681205749512 seconds, solution distance = 0.05806039214042258
Finished cycle #57 in 0.23853373527526855 seconds, solution distance = 0.0543016349872083
Finished cycle #58 in 0.24446892738342285 seconds, solution distance = 0.050792355429262415
Finished cycle #59 in 0.23846030235290527 seconds, solution distance = 0.04751525941490797
Finished cycle #60 in 0.23834943771362305 seconds, solution distance = 0.044454484600144895
Finished cycle #61 in 0.24232697486877441 seconds, solution distance = 0.04159298664174571
Finished cycle #62 in 0.23842740058898926 seconds, solution distance = 0.0389188115968615
Finished cycle #63 in 0.24158263206481934 seconds, solution distance = 0.03641910755728617
Finished cycle #64 in 0.24176406860351562 seconds, solution distance = 0.03408188475658491
Finished cycle #65 in 0.24629855155944824 seconds, solution distance = 0.03189605043228383
Finished cycle #66 in 0.23747467994689941 seconds, solution distance = 0.029851355475425834
Finished cycle #67 in 0.24113821983337402 seconds, solution distance = 0.027938308926213296
Finished cycle #68 in 0.24250006675720215 seconds, solution distance = 0.02614812496521779
Finished cycle #69 in 0.2368030548095703 seconds, solution distance = 0.024472707091931056
Finished cycle #70 in 0.24219918251037598 seconds, solution distance = 0.022904506785693002
Finished cycle #71 in 0.23986268043518066 seconds, solution distance = 0.021436548979984593
Finished cycle #72 in 0.24063372611999512 seconds, solution distance = 0.02006369692858101
Finished cycle #73 in 0.24188923835754395 seconds, solution distance = 0.01877843821991476
Finished cycle #74 in 0.24191570281982422 seconds, solution distance = 0.01757256485253933
Finished cycle #75 in 0.23726272583007812 seconds, solution distance = 0.016443733161427332
Finished cycle #76 in 0.24784588813781738 seconds, solution distance = 0.015386928487888696
Finished cycle #77 in 0.24249696731567383 seconds, solution distance = 0.014398454963458818
Finished cycle #78 in 0.2388439178466797 seconds, solution distance = 0.013473205667235533
Finished cycle #79 in 0.23897767066955566 seconds, solution distance = 0.012606505619487507
Finished cycle #80 in 0.23634552955627441 seconds, solution distance = 0.011794968634792014
Finished cycle #81 in 0.23593401908874512 seconds, solution distance = 0.011035290447981794
Finished cycle #82 in 0.24188995361328125 seconds, solution distance = 0.010323520782613116
Finished cycle #83 in 0.2406473159790039 seconds, solution distance = 0.009657068564937532
Finished cycle #84 in 0.23662972450256348 seconds, solution distance = 0.009033021861213797
Finished cycle #85 in 0.24515485763549805 seconds, solution distance = 0.008448680465587444
Finished cycle #86 in 0.24194121360778809 seconds, solution distance = 0.007901529967000442
Finished cycle #87 in 0.24025249481201172 seconds, solution distance = 0.007389222628706449
Finished cycle #88 in 0.23914432525634766 seconds, solution distance = 0.0069095629369329
Finished cycle #89 in 0.2426466941833496 seconds, solution distance = 0.006460495805733046
Finished cycle #90 in 0.23419928550720215 seconds, solution distance = 0.00604009682174933
Finished cycle #91 in 0.24608159065246582 seconds, solution distance = 0.005646562955103462
Finished cycle #92 in 0.2363889217376709 seconds, solution distance = 0.00527820455410577
Finished cycle #93 in 0.23595285415649414 seconds, solution distance = 0.004933437991201828
Finished cycle #94 in 0.24736976623535156 seconds, solution distance = 0.004610778604646981
Finished cycle #95 in 0.2406766414642334 seconds, solution distance = 0.004308834859578781
Finished cycle #96 in 0.2429969310760498 seconds, solution distance = 0.004026302266076698
Finished cycle #97 in 0.2385423183441162 seconds, solution distance = 0.003761957277351513
Finished cycle #98 in 0.23572444915771484 seconds, solution distance = 0.0035146519986142266
Finished cycle #99 in 0.23773670196533203 seconds, solution distance = 0.0032833094678750285
Finished cycle #100 in 0.24480390548706055 seconds, solution distance = 0.0030669193503207737
Finished cycle #101 in 0.23711705207824707 seconds, solution distance = 0.0028645339391815128
Finished cycle #102 in 0.23744726181030273 seconds, solution distance = 0.0026752644036172057
Finished cycle #103 in 0.23840546607971191 seconds, solution distance = 0.0024982772444062107
Finished cycle #104 in 0.23538708686828613 seconds, solution distance = 0.0023328323511329074
Finished cycle #105 in 0.23458385467529297 seconds, solution distance = 0.002178333119072562
Finished cycle #106 in 0.23614239692687988 seconds, solution distance = 0.002033848779593228
Finished cycle #107 in 0.2383708953857422 seconds, solution distance = 0.0018987560781837942
Finished cycle #108 in 0.23924636840820312 seconds, solution distance = 0.001772464733409862
Finished cycle #109 in 0.24867653846740723 seconds, solution distance = 0.0016544173642891735
Finished cycle #110 in 0.23617959022521973 seconds, solution distance = 0.0015440893104674558
Finished cycle #111 in 0.23368191719055176 seconds, solution distance = 0.001440987570251906
Finished cycle #112 in 0.24388575553894043 seconds, solution distance = 0.0013446493424176253
Finished cycle #113 in 0.24480247497558594 seconds, solution distance = 0.001254640439277921
Finished cycle #114 in 0.23627519607543945 seconds, solution distance = 0.0011705536868369393
Finished cycle #115 in 0.23915648460388184 seconds, solution distance = 0.0010920073625086957
Finished cycle #116 in 0.24079298973083496 seconds, solution distance = 0.0010186436927313025
Finished cycle #117 in 0.23693060874938965 seconds, solution distance = 0.0009501274203458365
Converged!
Solving took 27.963370084762573 seconds.

# Solve a short, finite horizon version
par_finite = init_risky_contrib.copy()

# Four period model
par_finite["PermGroFac"] = [2.0, 1.0, 0.1, 1.0]
par_finite["PermShkStd"] = [0.1, 0.1, 0.0, 0.0]
par_finite["TranShkStd"] = [0.2, 0.2, 0.0, 0.0]
par_finite["AdjustPrb"] = [0.5, 0.5, 1.0, 1.0]
par_finite["WithdrawTax"] = [0.1, 0.1, 0.0, 0.0]
par_finite["LivPrb"] = [1.0, 1.0, 1.0, 1.0]
par_finite["T_cycle"] = 4
par_finite["T_retire"] = 0
par_finite["T_age"] = 4

# Adjust discounting and returns distribution so that they make sense in a
# 4-period model
par_finite["DiscFac"] = 0.95**15
par_finite["Rfree"] = 4 * [1.03**15]
par_finite["RiskyAvg"] = 1.08**15  # Average return of the risky asset
par_finite["RiskyStd"] = 0.20 * np.sqrt(15)  # Standard deviation of (log) risky returns


# Create and solve
contrib_agent = RiskyContribConsumerType(**par_finite)
print("Now solving")
t0 = time()
contrib_agent.solve()
t1 = time()
print("Solving took " + str(t1 - t0) + " seconds.")

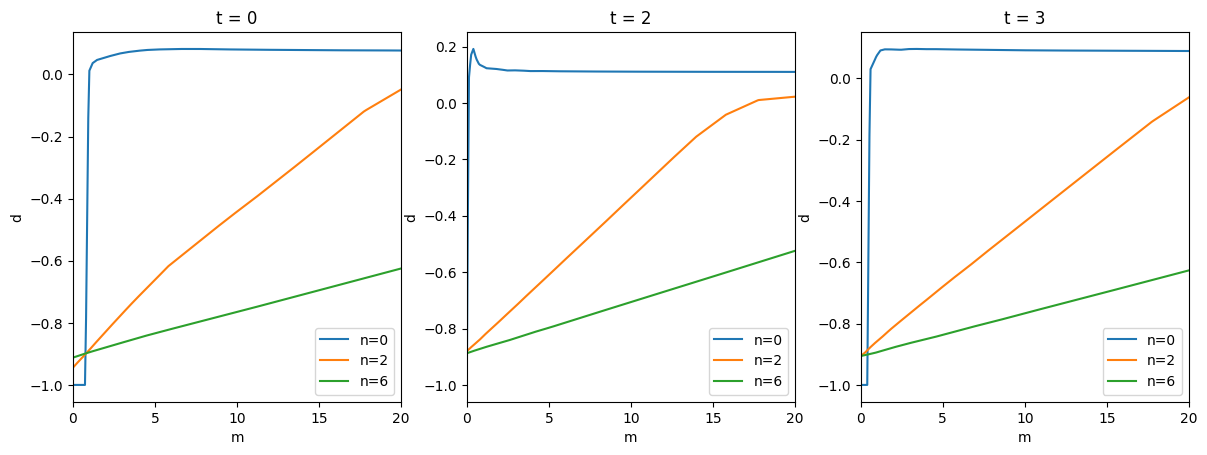
# Plot Policy functions
periods = [0, 2, 3]

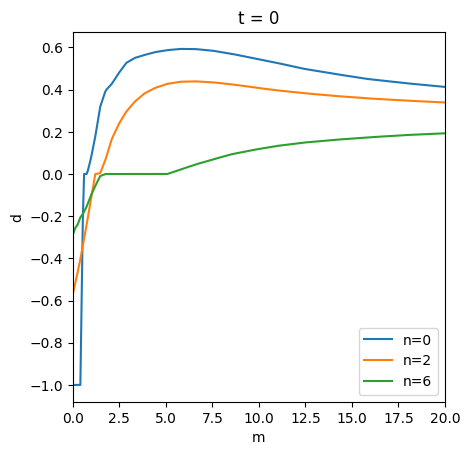
dfracFunc = [contrib_agent.solution[t].stage_sols["Reb"].dfracFunc_Adj for t in periods]
ShareFunc = [contrib_agent.solution[t].stage_sols["Sha"].ShareFunc_Adj for t in periods]
cFuncFxd = [contrib_agent.solution[t].stage_sols["Cns"].cFunc for t in periods]

# Rebalancing
plot_slices_3d(
    dfracFunc,
    0,
    mMax,
    y_slices=n_slices,
    y_name="n",
    titles=["t = " + str(t) for t in periods],
    ax_labs=["m", "d"],
)
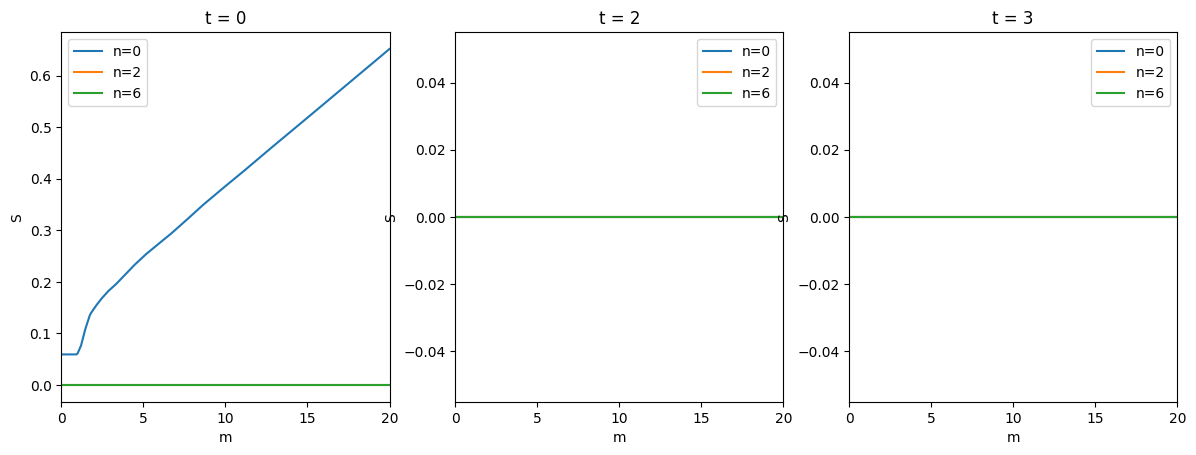
# Share
plot_slices_3d(
    ShareFunc,
    0,
    mMax,
    y_slices=n_slices,
    y_name="n",
    titles=["t = " + str(t) for t in periods],
    ax_labs=["m", "S"],
)
# Consumption
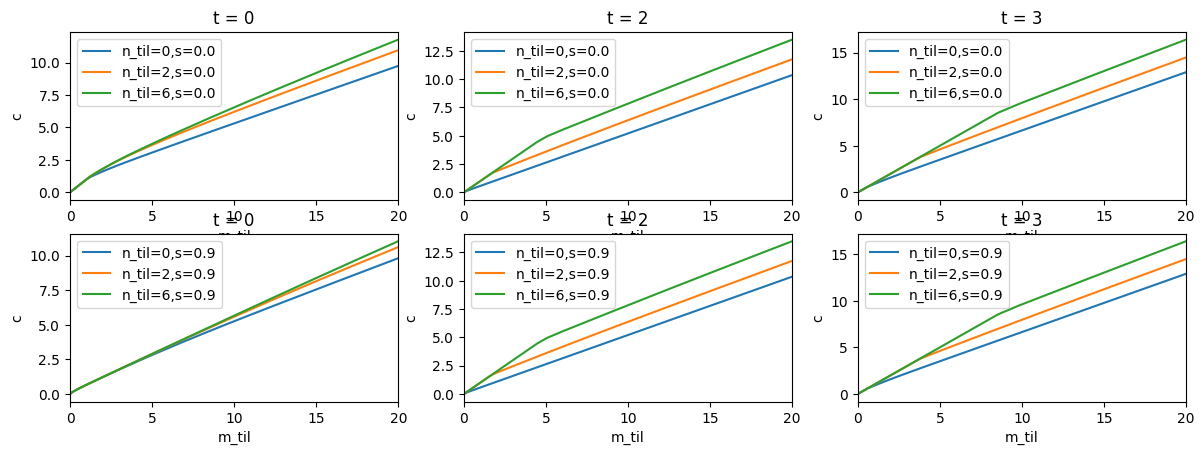
plot_slices_4d(
    cFuncFxd,
    0,
    mMax,
    y_slices=n_slices,
    w_slices=shares,
    slice_names=["n_til", "s"],
    titles=["t = " + str(t) for t in periods],
    ax_labs=["m_til", "c"],
)

Now solving
Solving took 2.3705382347106934 seconds.

contrib_agent.track_vars = [
    "pLvl",
    "t_age",
    "Adjust",
    "mNrm",
    "nNrm",
    "mNrmTilde",
    "nNrmTilde",
    "aNrm",
    "cNrm",
    "Share",
    "dfrac",
]
contrib_agent.T_sim = 4
contrib_agent.AgentCount = 10
contrib_agent.initialize_sim()
contrib_agent.simulate()

import pandas as pd

df = contrib_agent.history

# Add an id to the simulation results
agent_id = np.arange(contrib_agent.AgentCount)
df["id"] = np.tile(agent_id, (contrib_agent.T_sim, 1))

# Flatten variables
df = {k: v.flatten(order="F") for k, v in df.items()}

# Make dataframe
df = pd.DataFrame(df)