This page was generated from examples/ConsPortfolioModel/RiskyAssetConsumerType.ipynb.
Interactive online version: Binder badge. Download notebook.

Assets with Risky Returns: Portfolio Choice#

[1]:

from time import time

from HARK.ConsumptionSaving.ConsIndShockModel import (
    IndShockConsumerType,
    IndShockConsumerType_constructors_default,
)
from HARK.ConsumptionSaving.ConsPortfolioModel import (
    PortfolioConsumerType,
    init_portfolio,
)
from HARK.ConsumptionSaving.ConsRiskyAssetModel import (
    RiskyAssetConsumerType,
    IndShockRiskyAssetConsumerType_constructor_default,
)
from HARK.utilities import plot_funcs, plot_funcs_der
import matplotlib.pyplot as plt

[2]:

mystr = lambda number: f"{number:.4f}"

Idiosyncratic Income Shocks Consumer Type#

[3]:

# Make a dictionary for the idiosyncratic shocks type that uses common values from the portfolio type
common_dict = init_portfolio.copy()
common_dict["constructors"] = IndShockConsumerType_constructors_default
common_dict["CRRA"] = 5.0  # but make them pretty risk averse

[4]:

# Make and solve an example consumer with idiosyncratic income shocks
# Use init_portfolio parameters to compare to results of PortfolioConsumerType
IndShockExample = IndShockConsumerType(**common_dict)
IndShockExample.cycles = 0  # Make this type have an infinite horizon

[5]:

start_time = time()
IndShockExample.solve()
end_time = time()
print(
    "Solving a consumer with idiosyncratic shocks took "
    + mystr(end_time - start_time)
    + " seconds.",
)
IndShockExample.unpack("cFunc")

Solving a consumer with idiosyncratic shocks took 0.4361 seconds.

[6]:

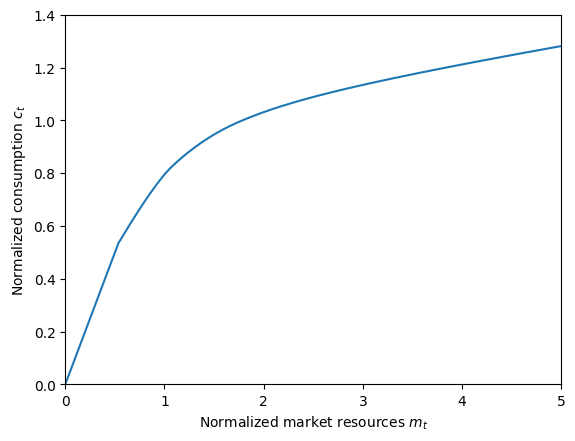
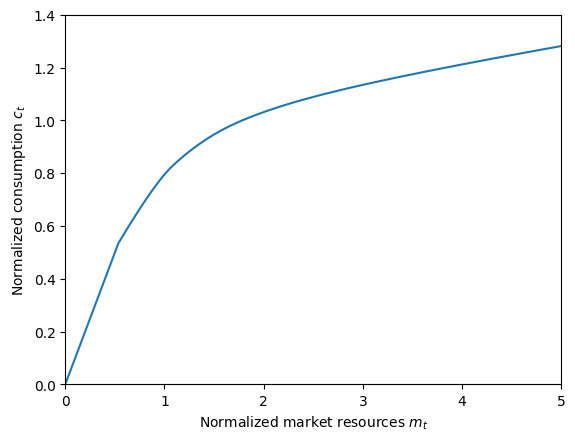
# Plot the consumption function and MPC for the infinite horizon consumer
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 1.4)
plot_funcs(IndShockExample.cFunc[0], 0.0, 5.0)
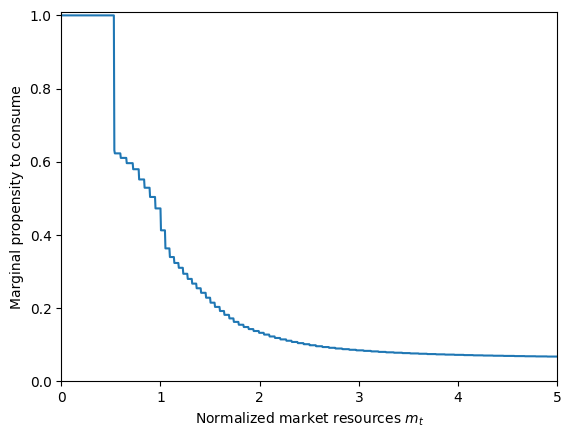
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Marginal propensity to consume")
plt.ylim(0.0, 1.01)
plot_funcs_der(IndShockExample.cFunc[0], 0.0, 5.0)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_7_0.png
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_7_1.png

Risky Return Consumer Type#

[7]:

# Make and solve an example consumer with risky returns to savings
# Use init_portfolio parameters to compare to results of PortfolioConsumerType
temp_dict = common_dict.copy()
temp_dict["constructors"] = IndShockRiskyAssetConsumerType_constructor_default
RiskyReturnExample = RiskyAssetConsumerType(**temp_dict)
RiskyReturnExample.cycles = 0  # Make this type have an infinite horizon

[8]:

start_time = time()
RiskyReturnExample.solve()
end_time = time()
print(
    "Solving a consumer with risky returns took "
    + mystr(end_time - start_time)
    + " seconds.",
)
RiskyReturnExample.unpack("cFunc")

Solving a consumer with risky returns took 3.4542 seconds.

[9]:

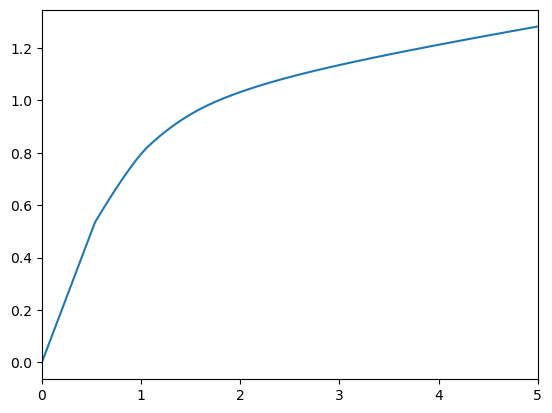
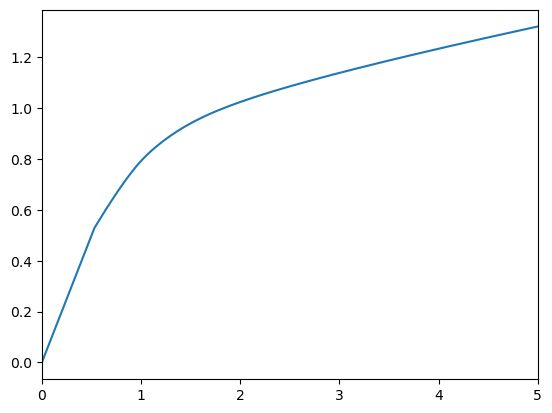
# Plot the consumption function and MPC for the risky asset consumer
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 1.4)
plot_funcs(RiskyReturnExample.cFunc[0], 0.0, 5.0)
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Marginal propensity to consume")
plt.ylim(0.0, 1.01)
plot_funcs_der(RiskyReturnExample.cFunc[0], 0.0, 5.0)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_11_0.png
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_11_1.png

Compare Idiosyncratic Income Shocks with Risky Return#

[10]:

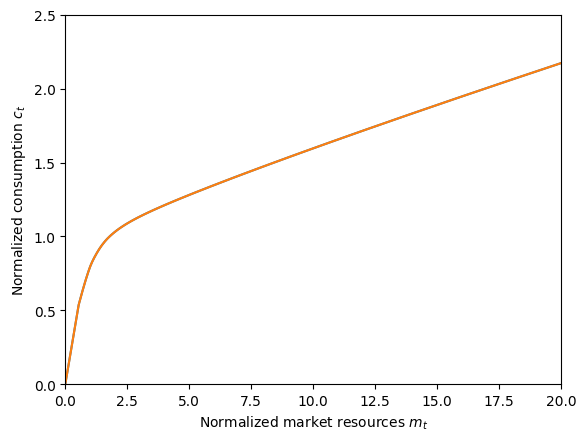
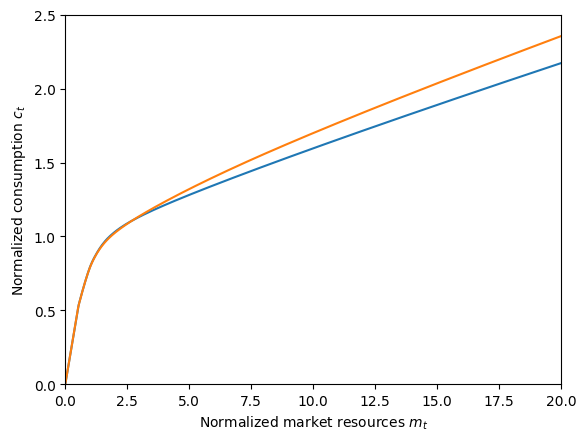
# Compare the consumption functions for the various agents in this notebook.
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 2.5)
plot_funcs(
    [
        IndShockExample.cFunc[0],  # blue
        RiskyReturnExample.cFunc[0],  # orange
    ],
    0.0,
    20.0,
)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_13_0.png

Risky Return Consumer Type with Portfolio Choice#

[11]:

# Make and solve an example risky consumer with a portfolio choice
temp_dict["PortfolioBool"] = True
PortfolioChoiceExample = RiskyAssetConsumerType(**temp_dict)
PortfolioChoiceExample.cycles = 0  # Make this type have an infinite horizon

[12]:

start_time = time()
PortfolioChoiceExample.solve()
end_time = time()
print(
    "Solving a consumer with risky returns and portfolio choice took "
    + mystr(end_time - start_time)
    + " seconds.",
)
PortfolioChoiceExample.unpack("cFunc")
PortfolioChoiceExample.unpack("ShareFunc")

Solving a consumer with risky returns and portfolio choice took 3.4221 seconds.

[13]:

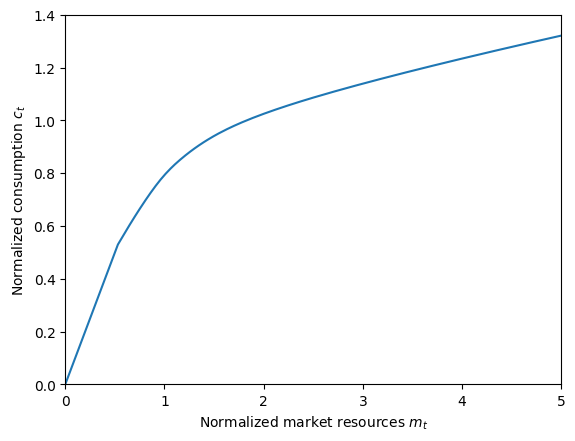
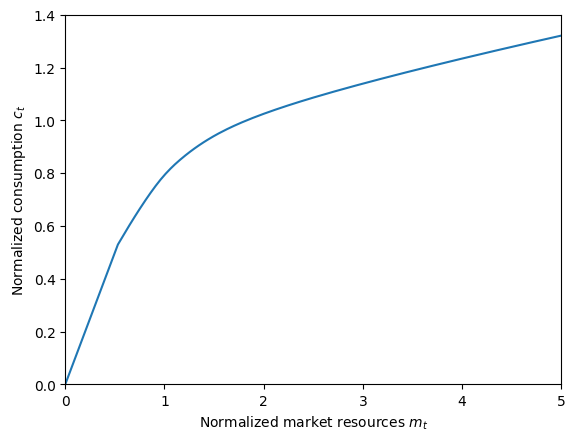
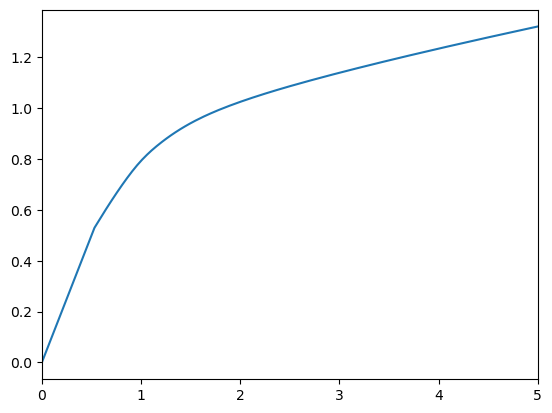
# Plot the consumption function and MPC for the portfolio choice consumer
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 1.4)
plot_funcs(PortfolioChoiceExample.cFunc, 0.0, 5.0)
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Marginal propensity to consume")
plt.ylim(0.0, 1.01)
plot_funcs_der(PortfolioChoiceExample.cFunc, 0.0, 5.0)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_17_0.png
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_17_1.png 
[14]:

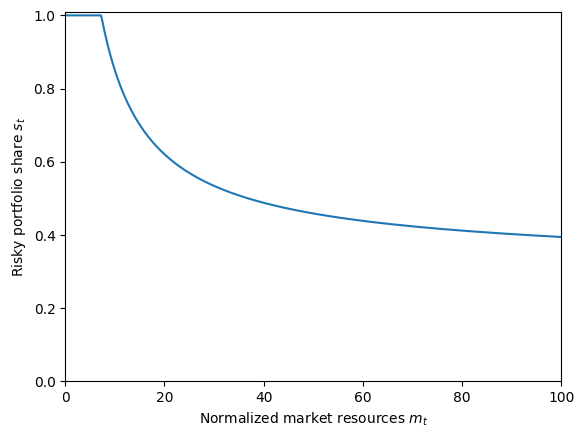
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Risky portfolio share $s_t$")
plt.ylim(0.0, 1.01)
plot_funcs(PortfolioChoiceExample.ShareFunc, 0.0, 100.0)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_18_0.png

Compare Income Shocks, Risky Return, and RR w/ Portfolio Choice#

[15]:

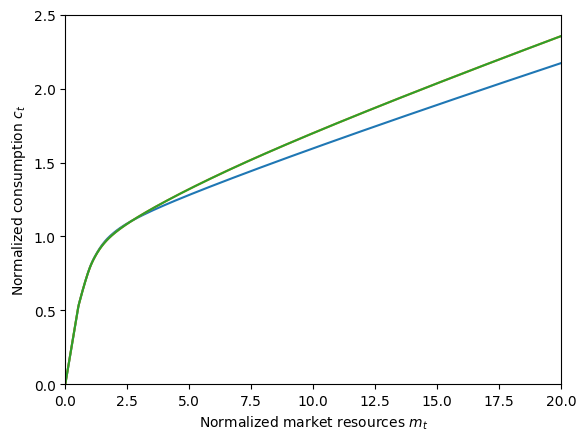
# Compare the consumption functions for the various agents in this notebook.
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 2.5)
plot_funcs(
    [
        IndShockExample.cFunc[0],  # blue
        RiskyReturnExample.cFunc[0],  # orange
        PortfolioChoiceExample.cFunc[0],  # green
    ],
    0.0,
    20.0,
)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_20_0.png

Portfolio Consumer Type#

[16]:

# Make and solve an example portfolio choice consumer
PortfolioTypeExample = PortfolioConsumerType(
    CRRA=5.0
)  # default parameters with higher risk aversion
PortfolioTypeExample.cycles = 0  # Make this type has an infinite horizon

[17]:

start_time = time()
PortfolioTypeExample.solve()
end_time = time()
print(
    "Solving a consumer with portfolio choice took "
    + mystr(end_time - start_time)
    + " seconds.",
)
PortfolioTypeExample.unpack("cFuncAdj")
PortfolioTypeExample.unpack("ShareFuncAdj")

Solving a consumer with portfolio choice took 10.4243 seconds.

[18]:

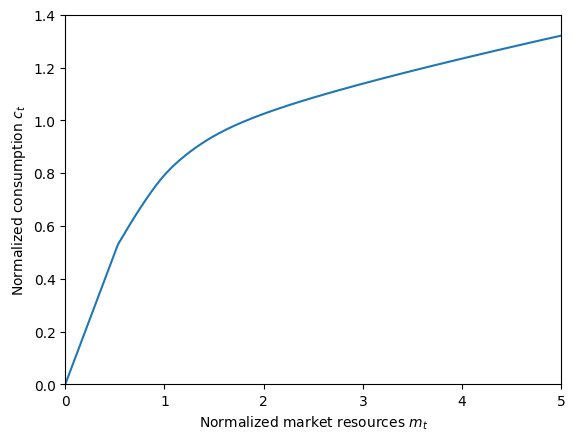
# Plot the consumption function and MPC for the portfolio choice consumer
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 1.4)
plot_funcs(PortfolioTypeExample.cFuncAdj[0], 0.0, 5.0)
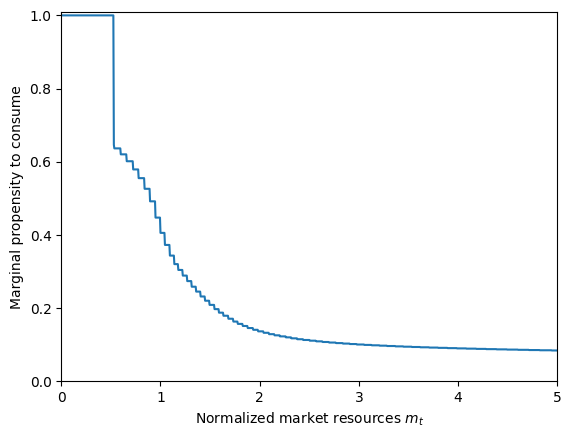
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Marginal propensity to consume")
plt.ylim(0.0, 1.01)
plot_funcs_der(PortfolioTypeExample.cFuncAdj[0], 0.0, 5.0)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_24_0.png
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_24_1.png

Compare RR w/ Portfolio Choice vs Portfolio Choice Type#

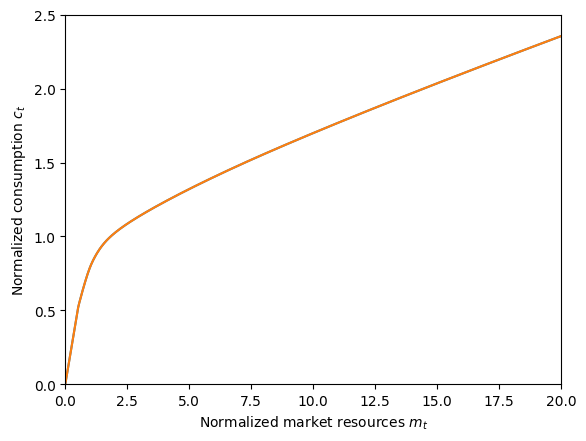
[19]:

# Compare the consumption functions for the various portfolio choice types.
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 2.5)
plot_funcs(
    [
        PortfolioTypeExample.cFuncAdj[0],  # blue
        PortfolioChoiceExample.cFunc[0],  # orange
    ],
    0.0,
    20.0,
)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_26_0.png 
[20]:

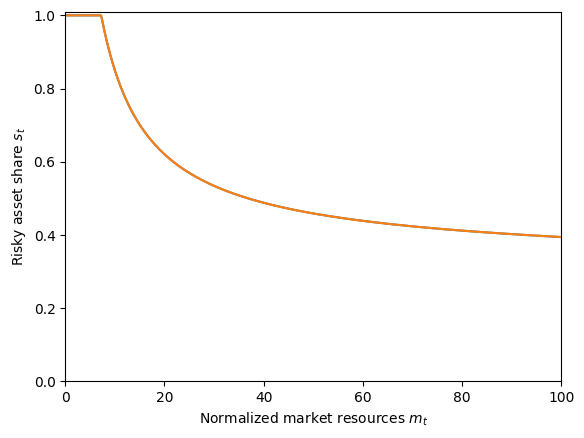
# Compare the share functions for the various portfolio choice types.
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Risky asset share $s_t$")
plt.ylim(0.0, 1.01)
plot_funcs(
    [
        PortfolioTypeExample.ShareFuncAdj[0],  # blue
        PortfolioChoiceExample.ShareFunc[0],  # orange
    ],
    0,
    100,
)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_27_0.png

Risky Return Given Fixed Portfolio Share#

[21]:

FixedShareExample = RiskyAssetConsumerType(**temp_dict)
FixedShareExample.assign_parameters(RiskyShareFixed=0.0, PortfolioBool=False)
FixedShareExample.update()
FixedShareExample.cycles = 0

[22]:

start_time = time()
FixedShareExample.solve()
end_time = time()
print(
    "Solving a consumer with fixed portfolio share took "
    + mystr(end_time - start_time)
    + " seconds.",
)
FixedShareExample.unpack("cFunc")

Solving a consumer with fixed portfolio share took 0.5191 seconds.

[23]:

# Plot the consumption function and MPC for the infinite horizon consumer
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 1.4)
plot_funcs(FixedShareExample.cFunc[0], 0.0, 5.0)
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Marginal propensity to consume")
plt.ylim(0.0, 1.01)
plot_funcs_der(FixedShareExample.cFunc[0], 0.0, 5.0)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_31_0.png
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_31_1.png

Compare Idiosyncratic Shock Type vs Fixed Share at 0.0 Type#

[24]:

# Compare the consumption functions for the various idiosyncratic shocks
plt.xlabel(r"Normalized market resources $m_t$")
plt.ylabel(r"Normalized consumption $c_t$")
plt.ylim(0.0, 2.5)
plot_funcs(
    [
        IndShockExample.cFunc[0],  # blue
        FixedShareExample.cFunc[0],  # orange
    ],
    0.0,
    20.0,
)
../../_images/examples_ConsPortfolioModel_RiskyAssetConsumerType_33_0.png 
[ ]: