Interactive online version:
Solving Krusell Smith Model with HARK and SSJ#
By William Du
[1]:
import time
import matplotlib.pyplot as plt
import numpy as np
from scipy import optimize
from sequence_jacobian import create_model, simple # functions
from sequence_jacobian.classes import JacobianDict, SteadyStateDict
from HARK.ConsumptionSaving.ConsNewKeynesianModel import NewKeynesianConsumerType
Calibration and setup#
This notebook uses the HARK toolkit to solve Krusell and Smith (1998), applying the Sequence Space Jacobian and SSJ toolkit.
Firm setup#
Collect calibration for the production economy in a dictionary.
[2]:
calibration = {
"eis": 1, # Elasticity of intertemporal substitution
"delta": 0.025, # Depreciation rate
"alpha": 0.11, # Capital share of income
"L_ss": 1.0, # Steady state labor
"Y_ss": 1.0, # Steady state output
"r_ss": 0.01, # Steady state real interest rate
}
Steady State Capital#
Find steady state capital (K_ss) and productivity (Z) implied by the firm’s first order condition, aggregate resource constraint and the above steady state values of labor (L_ss), the real interest rate (r_ss) and output (Y_ss).
[3]:
from scipy.optimize import root
def your_funcs(X):
L_ss = calibration["L_ss"]
alpha = calibration["alpha"]
delta = calibration["delta"]
r_ss = calibration["r_ss"]
Y_ss = calibration["Y_ss"]
K, Z = X
# Firms first order condition and aggregate resource constraint
f = [
alpha * Z * (K / L_ss) ** (alpha - 1) - delta - r_ss, # r_ss = MPK
Z * K**alpha * L_ss ** (1 - alpha) - Y_ss, # Y = Z*F(K,L)
]
return f
sol = root(your_funcs, [1.0, 1.0]) # find roots
K_ss, Z_ss = sol.x
calibration["K_ss"] = K_ss
calibration["Z_ss"] = Z_ss
[4]:
print(sol)
message: The solution converged.
success: True
status: 1
fun: [ 1.749e-14 -5.218e-15]
x: [ 3.143e+00 8.816e-01]
method: hybr
nfev: 14
fjac: [[-3.675e-01 9.300e-01]
[-9.300e-01 -3.675e-01]]
r: [ 3.906e-02 1.143e+00 -3.236e-01]
qtf: [-4.533e-12 -5.621e-12]
Double check the roots we find produce our chosen steady state values.
[5]:
def firm(
K,
Z,
L_ss=calibration["L_ss"],
alpha=calibration["alpha"],
delta=calibration["delta"],
):
r = alpha * Z * (K / L_ss) ** (alpha - 1) - delta
w = (1 - alpha) * Z * (K / L_ss) ** alpha
Y = Z * K**alpha * L_ss ** (1 - alpha)
return r, w, Y
r_ss, w_ss, Y_ss = firm(sol.x[0], sol.x[1])
calibration["w_ss"] = w_ss
[6]:
print("--------------------------------------+------------")
print(f"Steady state capital | {K_ss:.4f}")
print(f"Steady state output | {Y_ss:.4f}")
print(f"Steady state real interest rate | {r_ss:.4f}")
print(f"Steady state wage | {w_ss:.4f}")
print("--------------------------------------+------------")
--------------------------------------+------------
Steady state capital | 3.1429
Steady state output | 1.0000
Steady state real interest rate | 0.0100
Steady state wage | 0.8900
--------------------------------------+------------
HARK agent#
HARK represents agent problems where aggregate variables can affect an individual income process as instances of NewKeynesianConsumerType, a subclass of AgentType (see A Gentle Introduction to HARK).
Instances of the NewKeynesianConsumerType class contain functions that solve policy functions of optimizing agents and compute Jacobian matrices in response to a policy shocks using the SSJ toolkit.
NOTE: NewKeynesianConsumerType is still a microeconomic agent solving an income fluctuation problem. The only difference from `IndShockConsumerType <https://docs.econ-ark.org/examples/HowWeSolveIndShockConsumerType/HowWeSolveIndShockConsumerType.html>`__ is that additional aggregate labour income variables are passed to the agent’s income process. This allows the agent’s problem to be defined within a general equilibrium framework such as (but not restricted to) HANK.
NOTE: Researchers can also create their own agent types by subclassing AgentType. See HARK’s documentation for more information.
To create an instance of NewKeynesianConsumerType, first specify parameters in a dictionary. To start, we use a discount factor of 0.98.
[7]:
L_ss = calibration["L_ss"]
w_ss = calibration["w_ss"]
r_ss = calibration["r_ss"]
HANK_Dict = {
# Individual agent 'preferences' (shared with perfect foresight model)
"CRRA": calibration["eis"], # Coefficient of relative risk aversion
"DiscFac": 0.98, # Intertemporal discount factor
"LivPrb": [0.99375], # Survival probability
# Individual lifcycle income process parameters
"PermGroFac": [1.00], # Permanent income growth factor
"PermShkStd": [0.06], # Standard deviation of log permanent shocks to income
"PermShkCount": 5, # Number of points in discrete approximation to permanent income shocks
"TranShkStd": [0.2], # Standard deviation of log transitory shocks to income
"TranShkCount": 5, # Number of points in discrete approximation to transitory income shocks
# Parameters related to unemployment and retirement
"UnempPrb": 0.0, # Probability of unemployment while working
"IncUnemp": 0.0, # Unemployment benefits replacement rate
"UnempPrbRet": 0.0000, # Probability of "unemployment" while retired
"IncUnempRet": 0.0, # "Unemployment" benefits when retired
"T_retire": 0.0, # Period of retirement (0 --> no retirement)
# Aggregates affecting the agent's decision
"Rfree": [(1 + r_ss)], # Interest factor for assets faced by agents
"wage": [w_ss], # Wage rate faced by agents
"tax_rate": [
0
], # set to 0.0 because we are going to assume that labor here is actually after tax income
"labor": [L_ss], # Aggregate (mean) labor supply
# Parameters for constructing "assets above minimum" grid
"aXtraMin": 0.0001, # Minimum end-of-period "assets above minimum" value
"aXtraMax": 2000, # Maximum end-of-period "assets above minimum" value
"aXtraCount": 200, # Number of points in the base grid of "assets above minimum"
# Exponential nesting factor when constructing "assets above minimum" grid
"aXtraNestFac": 3,
"aXtraExtra": None, # Additional values to add to aXtraGrid
# Transition matrix simulation parameters
"mCount": 200,
"mMax": 2000,
"mMin": 0.0001,
"mFac": 3,
}
Let’s create a temporary instance of a NewKeynesianConsumerType agent.
[8]:
tempAgent = NewKeynesianConsumerType(**HANK_Dict)
Given a discount factor, the agent will supply a steady state capital stock A_ss.
[9]:
A_ss = tempAgent.compute_steady_state()[0]
print(f"Steady state agent asset supply for beta = 0.98 is: {A_ss:.3f}")
Steady state agent asset supply for beta = 0.98 is: 0.231
Steady State Assets#
Since we are interested in computing a steady state equilibrium, we find discFac such that A_ss clears the asset market given that K_ss is the steady state firm capital demand.
[10]:
def A_ss_func(beta):
HANK_Dict["DiscFac"] = beta
# For a given value of beta, we need to re-create the Agent
Agent_func = NewKeynesianConsumerType(**HANK_Dict, verbose=False)
# And then solve for the steady state supply
A_ss = Agent_func.compute_steady_state()[0]
return A_ss
def ss_dif(beta):
return A_ss_func(beta) - Asset_target
start = time.time()
Asset_target = K_ss
DiscFac = optimize.brentq(ss_dif, 0.8, 0.9999)
print(f"Time taken to solve for steady state {time.time() - start:.3f} secs.")
Time taken to solve for steady state 11.408 secs.
We can now create the steady state agent using the general equilibrium discount factor.
[11]:
# Create a new agent
HANK_Dict["DiscFac"] = DiscFac
steadyHANK = NewKeynesianConsumerType(**HANK_Dict, verbose=False)
A_ss, C_ss = steadyHANK.compute_steady_state()
[12]:
# To make sure goods and asset markets clear
print(
"Final goods clearing:",
calibration["Y_ss"] - C_ss - calibration["delta"] * calibration["K_ss"],
)
print("Asset clearing:", A_ss - calibration["K_ss"])
Final goods clearing: 0.019151809710635556
Asset clearing: -4.28052704393167e-10
Computing Jacobians using SSJ#
With the steady state agent in hand, we can compute the Jacobians of the steady state HANK agent’s policy with respect to the aggregate state variables.
The calc_jacobian method of our NewKeynesianConsumerType agent computes the Jacobians of the steady state aggregate consumption (CJACW) and assets (AJACW) with respect to a pertubation of a specified variable.
Recall CJACW[s,t] is the time \(t\) response to a shock at time \(s\).
Here is an example where we shock the wage rate.
[13]:
start = time.time()
CJACW, AJACW = steadyHANK.calc_jacobian("wage", 300) # Wage jacobians
print(f"Time taken to compute wage Jacobians: {time.time() - start:.3f} seconds")
Time taken to compute wage Jacobians: 4.084 seconds
[14]:
plt.plot(CJACW.T[0], label="s=0")
plt.plot(CJACW.T[20], label="s=20")
plt.plot(CJACW.T[50], label="s=50")
plt.plot(CJACW.T[100], label="s=100")
plt.xlim(-2, 300)
plt.plot(np.arange(300), np.zeros(300), color="k")
plt.title("Consumption Jacobian (Wage) ")
plt.xlabel("Quarters")
plt.ylabel("Consumption response")
plt.legend()
plt.show()
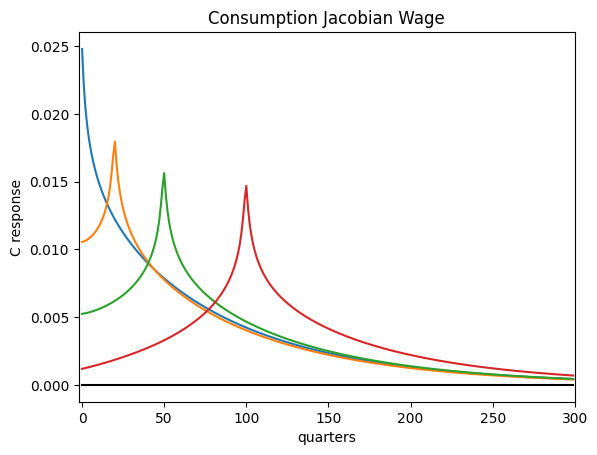
[15]:
start = time.time()
CJACR, AJACR = steadyHANK.calc_jacobian("Rfree", 300) # Rfree jacobians
print(
f"Time taken to compute return factor Jacobians: {time.time() - start:.3f} seconds"
)
Time taken to compute return factor Jacobians: 3.977 seconds
Here is an example where we shock the return factor.
[16]:
plt.plot(CJACR.T[0], label="s =0")
plt.plot(CJACR.T[20], label="s=20")
plt.plot(CJACR.T[50], label="s=50")
plt.plot(CJACR.T[100], label="s=100")
plt.plot(np.arange(300), np.zeros(300), color="k")
plt.title("Consumption Jacobian (Return Factor)")
plt.xlabel("Quarters")
plt.ylabel("Consumption response")
plt.show()
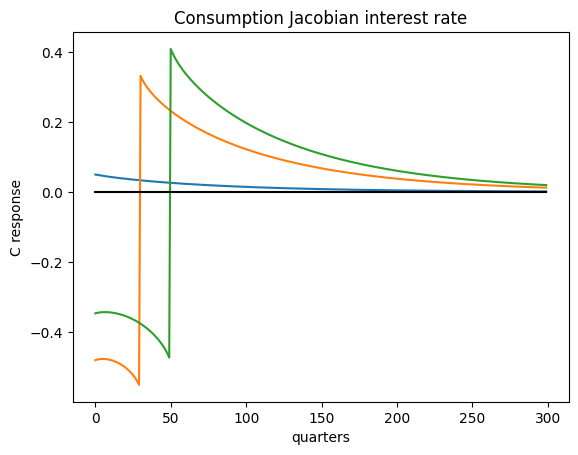
Let’s store the Jacobians in a dictionary for later use.
[17]:
# Store Jacobians in JacobianDict Object
Jacobian_Dict = JacobianDict(
{
"C": {
"w": CJACW,
"r": CJACR,
},
"A": {
"w": AJACW,
"r": AJACR,
},
},
)
# Construct SteadyStateDict object
SteadyState_Dict = SteadyStateDict(
{
"asset_mkt": 0.0,
"goods_mkt": 0.0,
"r": r_ss,
"Y": Y_ss,
"A": K_ss,
"C": C_ss,
"Z": Z_ss,
"delta": calibration["delta"],
"alpha": calibration["alpha"],
"L": L_ss,
"K": K_ss,
"w": w_ss,
},
)
Impulse Response Functions and Simulations#
[18]:
@simple
def firm(K, L, Z, alpha, delta):
r = alpha * Z * (K(-1) / L) ** (alpha - 1) - delta
w = (1 - alpha) * Z * (K(-1) / L) ** alpha
Y = Z * K(-1) ** alpha * L ** (1 - alpha)
return r, w, Y
@simple
def mkt_clearing(K, A, Y, C, delta):
asset_mkt = A - K
goods_mkt = Y - C - delta * K
return asset_mkt, goods_mkt
[19]:
ks = create_model([Jacobian_Dict, firm, mkt_clearing], name="Krusell-Smith")
Solving for Impulse Responses#
[20]:
T = 300 # Length of the IRF
rho_Z = 0.8 # Persistence of IRF shock
dZ = 0.001 * Z_ss * rho_Z ** np.arange(T)
shocks = {"Z": dZ}
inputs = ["Z"]
unknowns = ["K"]
targets = ["asset_mkt"]
irfs_Z = ks.solve_impulse_linear(SteadyState_Dict, unknowns, targets, shocks)
[21]:
def show_irfs(
irfs_list,
variables,
labels=[" "],
ylabel=r"Percentage point (dev. from ss)",
T_plot=50,
figsize=(18, 6),
):
if len(irfs_list) != len(labels):
labels = [" "] * len(irfs_list)
n_var = len(variables)
fig, ax = plt.subplots(1, n_var, figsize=figsize, sharex=True)
for i in range(n_var):
# plot all irfs
for j, irf in enumerate(irfs_list):
ax[i].plot(irf[variables[i]][:50] * 1e2, label=labels[j])
ax[i].set_title(variables[i])
ax[i].set_xlabel(r"Quarters")
if i == 0:
ax[i].set_ylabel(ylabel)
# ax[i].legend()
# ax[i].x
plt.tight_layout()
plt.show()
# plt.savefig("irf.png")
[22]:
# Impulse Responses to Productivity Shock
show_irfs([irfs_Z], ["Y", "C", "Z", "K", "r"])
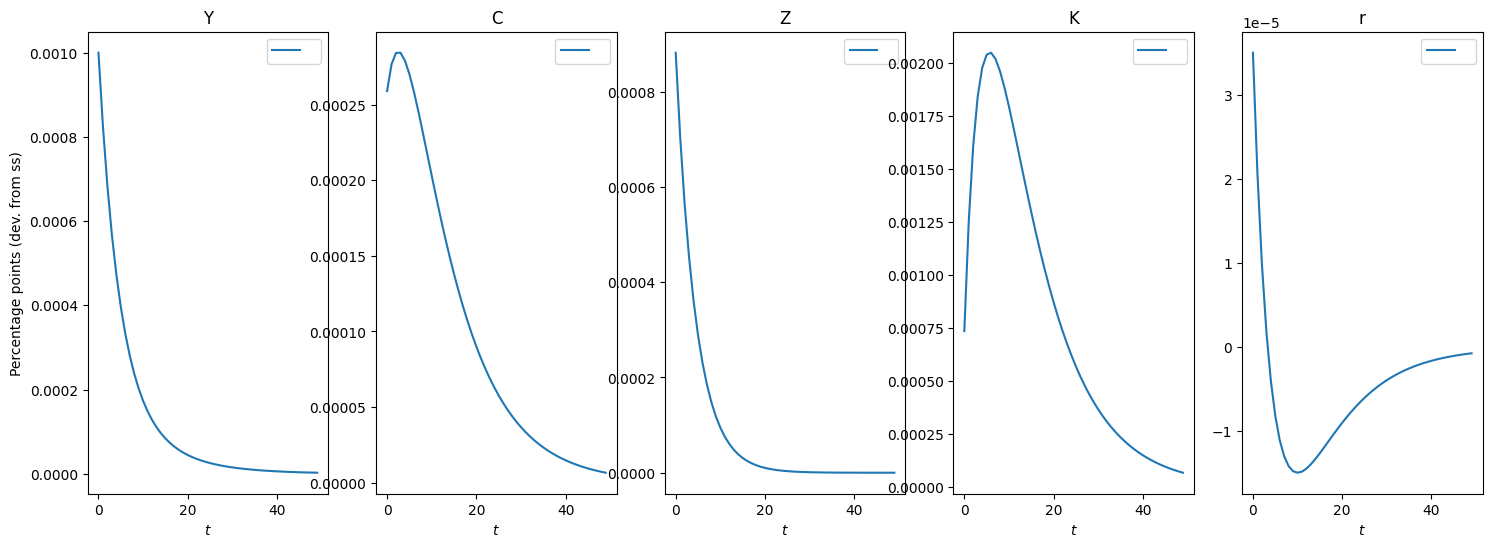
Simulating the model#
[23]:
from estimation.plots import plot_timeseries
from estimation.routines import simulate
[24]:
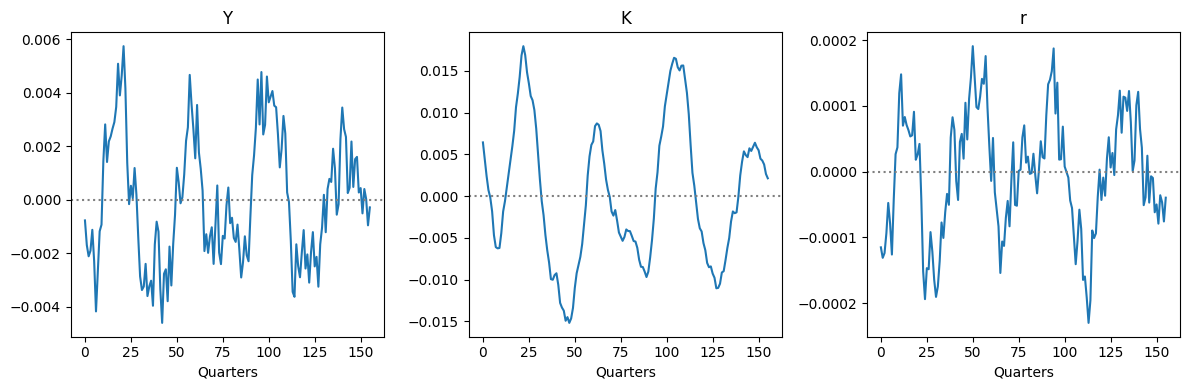
outputs = ["Y", "K", "r"]
sigmas = {"Z": 0.001}
rhos = {"Z": 0.8}
impulses = {}
for i in inputs:
own_shock = {i: sigmas[i] * rhos[i] ** np.arange(T)}
impulses[i] = ks.solve_impulse_linear(
SteadyState_Dict,
unknowns,
targets,
own_shock,
)
T_sim = 156 # 39 years, as in the original SW (2007) sample
data_simul = simulate(list(impulses.values()), outputs, T_sim)
plot_timeseries(data_simul, (1, 3), figsize=(12, 4))